BMW I4 and linear dynamic Truchet tilings

Isn’t this BMW I4 a beauty? The perfect motivation to start a journey into a little optimization problem:

How to manipulate traditional Truchet tiles so that the resulting tiling resembles the Ultimate Driving Machine?

Truchet tiles are a well known niche in math because they form a foundation for a lot of interesting questions. The basic theory: You have four simple tiles:

Since every tile is 50% black and 50% white a resulting tiling can only resemble a grey area if viewed from afar. In order to depict images it is necessary to manipulate the proportion of black vs. white.

Just envision one Truchet tile as a dot in a black-and-white rater image:

The trick is now to manipulate the tiles so that they can approximate the grey shade of a raster point.

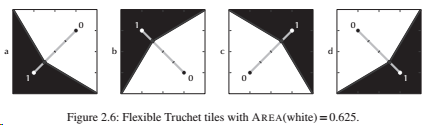
Source: Bosch, Robert. Opt Art: From Mathematical Optimization to Visual Design (p. 6). Princeton University Press.

The black half is intersected by a diagonal: \((0,1)\). Along this line the threshold for black can be moved up and down.

\(t = 0 \Leftrightarrow P(0.25, 0.25)\): maximal brightness.
\(t = 1 \Leftrightarrow P(0.75, 0.75)\): maximal darkness.

The brightness of a tile is only depending on the parameter \(t \in (0, 1)\).

As a result the polygon ABPC encloses an area which is proportional to the darkness of the tile. This is a very simple linear dependency and can be easily modelled.

If a is the length of the tile and t is our ‘black’ parameter, then the math is: $$ t’ = \sqrt{2} \\ y_1 = - \frac{a-t’}{t’}x + a \\ y_2 = - \frac{t’}{a-t’}x + \frac{at’}{a-t’} \\ $$

Enough theory, let’s see what can be done with this simple model.

Application of model

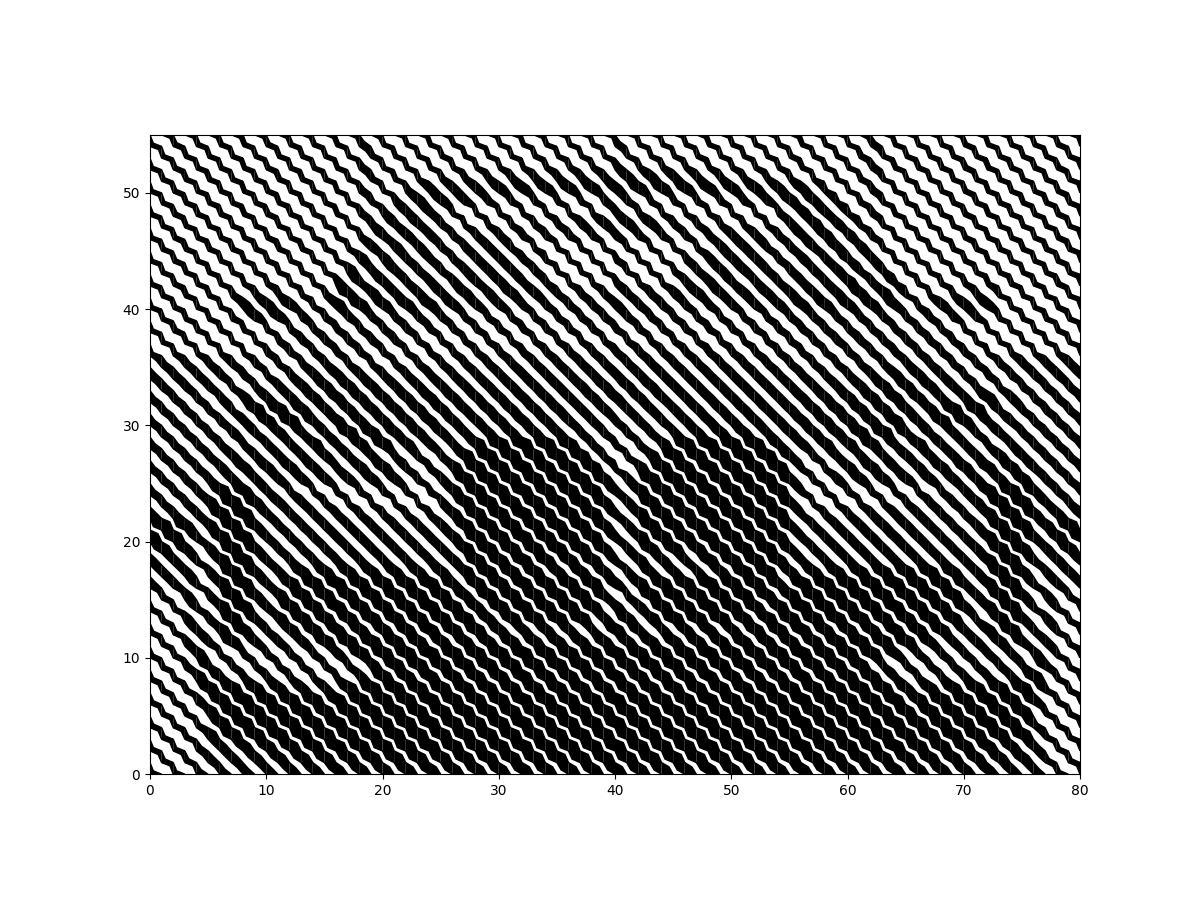
Isn’t this a beautiful combination of math, programming and design?

If you are interested in the Python code contact me via mail.