Fishy Affine Transformation

13 Mar, 2017

Fishy Affine Transformation

While working on the kaggle competition https://www.kaggle.com/c/the-nature-conservancy-fisheries-monitoring I hit the point when I wanted to align fish based on an annotation at the fish’s head and tail, so that the fish is centered in the image, always in the same orientation and distracting picture information is minimized. This required:

finding the fish (thanks Nathaniel Shimoni for annotating)
centering
rotatating
cropping

Mathematically the challenge is to find the associated Affine Transformation. After years of working in a managerial role my linear algebra skills are a bit rusty so I decided to invest the weekend.

Affine Transformation

Wolfram: An affine transformation is any transformation that preserves collinearity (i.e., all points lying on a line initially still lie on a line after transformation) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint after transformation).

I decided to use CV2 after hitting the wall with several other tools. It was not the most convenient choice, but eventually it got me there. CV2 uses (2x3) transformation matrices for affine transformations so I had to adjust my 2d vectors accordingly.

The reason: Homogeneous Coordinates.

To combine rotation and translation in one operation one extra dimension is needed more than the model requires. For planar things this is 3 components and for spatial things this is 4 components. The operators take 3 components and return 3 components requiring 3x3 matrices.

Using vector algebra with numpy requires some extra consideration but is possible. Basically a (2,) matrix represented the 2-dim vectors. Small letters denoted vector variables and caps matrices.

1. Finding the Fish

I used the annotations from labels produced by Nathaniel Shimoni and published on Kaggle (thanks for the great work!).

Using only fish with head and tail annotated, it was possible to get the vector representation of a fish as:

p_heads = np.array((img_data['annotations'][0]['x'], img_data['annotations'][0]['y']))
p_tails = np.array((img_data['annotations'][1]['x'], img_data['annotations'][1]['y']))
p_middle = (p_heads + p_tails)/2
v_fish = p_heads - p_tails

2. Centering

Centering fish is a basic translation in the 2-dim space.

    # translate to center of img
    img_center = np.array([img_height/2, img_width/2])
    t = img_center - p_middle  # translation vector
    t = np.reshape(t, (2,1))  # generate the 2x3 affine transformation matrix
    T = np.concatenate((np.identity(2), t), axis=1)

The respective transformation matrix is:

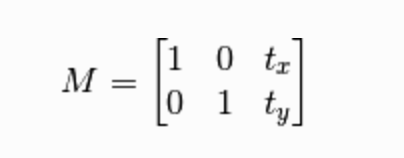
3. Rotating

First I needed to find the angle for rotation. I wanted to have the fish oriented parallel to the x-axis with the head always being on the right. The dot-product of two vectors provides the angle in between, so I had to ‘dot-product’ my fish vector with the x-axis:

def unit_vector(vector):
    """ Returns the unit vector of the vector."""
    return vector / np.linalg.norm(vector)

def angle_between(v1, v2):
    """ Returns the angle in radians between vectors 'v1' and 'v2'::

            >>> angle_between((1, 0, 0), (0, 1, 0))
            1.5707963267948966
            >>> angle_between((1, 0, 0), (1, 0, 0))
            0.0
            >>> angle_between((1, 0, 0), (-1, 0, 0))
            3.141592653589793
    """
    v1_u = unit_vector(v1)
    v2_u = unit_vector(v2)
    return np.arccos(np.clip(np.dot(v1_u, v2_u), -1.0, 1.0))

angle = np.rad2deg(angle_between((1, 0), v_fish))

Conveniently CV2 provides a function to find the necessary transformation matrix (cv2.getRotationMatrix2D).

A challenge was to find out, that the rotation angle returned always is between 0-180°, so the following conditional differentiation was necessary (rotation counter clockwise vs clockwise). It basically differentiates between the case that the head is above or below the tail:

    # get the Affine transformation matrix
    if p_heads[1] > p_tails[1]:  # head is above tail
        M = cv2.getRotationMatrix2D((p_middle[0], p_middle[1]), angle, 1)
    else:
        M = cv2.getRotationMatrix2D((p_middle[0], p_middle[1]), -angle, 1)

Putting it all together

Getting the resulting transformation from a translation and rotation mathematically translates to a matrix product and applying the resulting transformation matrix to the fish vector. To make the multiplication of a 2x3 tranlation matrix and a 2x3 rotation matrix possible the following steps were necesary (combination of two affine transformations):

allocate A1, A2, R matrices, all 3x3 identity matrices (eyes)
replace the top part of A1 and A2 with the transformation matrices T and M
get the resulting transformation (matrix product)
return the first two rows of R

So RR was my final transformation matrix.

    # compinte affine transform: make them 3x3
    # http://stackoverflow.com/questions/13557066/built-in-function-to-combine-affine-transforms-in-opencv
    A1 = np.identity(3)
    A2 = np.identity(3)
    R = np.identity(3)
    A1[:2] = T
    A2[:2] = M
    R = A1@A2
    RR = R[:2]

Getting the transformed image is now straightforward:

    dst = cv2.warpAffine(img, RR, (img_height, img_width))

The nice thing with this approach is that once you have got the final transformation matrix, all other points of interest can be transformed by this matrix, e.g. the head and tail annotations are transformed by the same matrix.

Result

The blue point marks the head and the red point the tail. You can see the fish positioned arbitrarily in the image. With the Affine Transformation the fish will be extracted and aligned. The result is being displayed in the left upper corner.

With this technique I was able to align my fish and feed it into my machine learning models.

Thanks for reading.

Disclaimer

I use http://stackoverflow.com/ a lot. Not every source is quoted properly. Other sources: https://www.kaggle.com/qiubit/the-nature-conservancy-fisheries-monitoring/crop-fish

#python #math #machine learning #ai