Linear Programming for Dummies 4

This is a collection of logic recipies for Mixed Integer Programming. It builds on Part3.

It is based on personal learning experience and focuses on application rather than theory. For a rigorous approach please refer to a textbook.

Logic Recipies

All variables here can only take boolean values: \(x_i, y \in{0, 1}\)
Let \(X_i\) stand for the proposition \(x_i=1\), anaolog for \(Y\).

if X then Y

$$ x \rightarrow y $$

Set of constraints: $$ y \ge x \\ $$

Example

You can launch satellite X only if you have chosen a compatible booster Y.

Y then X1 AND X2 (and vice versa)

$$ y \leftrightarrow x_1 \land x_2 $$ Set of constraints: $$ y \ge x_1 + x_2 -1\\ y \le x_1\\ y \le x_2\\ 0 \le y \le 1 \\ $$

Generalized with range constraint:
$$ y = x_1 \land … \land x_n\\ 0 \le \sum_i x_i -ny \le n-1\\ $$

Example

Y can be produced if and only if a machine X1 and worker X2 are available.”

Y then X1 OR X2 (and vice versa)

$$ y \leftrightarrow x_1 \lor x_2 $$ y if and only if x1 or x2 or both.

$$ y \le x_1 + x_2 \\ y \ge x_1\\ y \ge x_2\\ 0 \le y \le 1 \\ $$

generalized with range constraint:
$$ y = x_1 \lor … \lor x_n\\ 0 \le ny - \sum_i x_i \le n-1\\ $$

Example

Project Y can be funded if and only if project X1 or project X2, or both projects are funded.

XOR

$$ y \leftrightarrow x_1 \oplus x_2 $$ y if x1 or x2, but not both.

$$ y \le x_1 + x_2\\ y \ge x_1 - x_2\\ y \ge x_2 - x_1\\ y \le 2 - x_1 - x_2\\ 0 \le y \le 1\\ $$

Example

Packaging line Y can receive product from either processing line X1 or processing line X2.

Cheat Sheet

I helpful collection of recipies can be found here:

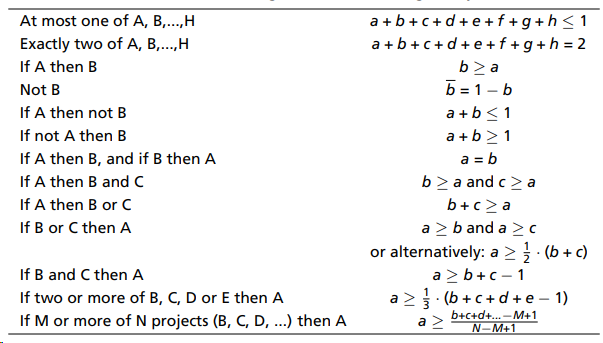
Summary

This collection is a living document. If you have a recipe to be included, please let me know. I am more than happy to extend the collection and cite the originator.