Normally you would be searching for the shortest path from A to B. At least this is what navigation systems do. But here we want to look at the opposite problem:

What is the longest possible path to get from A to B?

Wikipedia

The longest path problem is the problem of finding a simple path of maximum length in a given graph. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard.

We are looking for a simple path, i.e. every node must only be visited (maximal) once. This sounds familiar to the Traveling Salesman Problem. Indeed, the problem can be modelled in a similar form ¹:

Problem Formulation

$$ \max \sum_{(i,j)\in A} d_{i,j}x_{i,j}\\ $$ Network routing often gets modelled as a flow optimization problem. Hence, the typical flow balance constraints apply.

Node Flow Balance: flow in equals flow out of node: $$ \sum_{j|(j,i) \in A} x_{j,i} + b_i = \sum_{j|(i,j) \in A} x_{i,j}, \ \forall i \\ $$

Outflow of each node must only go to one arc/edge: $$ \sum_{j|(i,j) \in A} x_{i,j} \le 1 \ \forall i| i \ne \text{sink} \\ \sum_{j|(i,j) \in A} x_{i,j} = 0, \ i = \text{sink} \\ $$

Sub-tour elimination constraints are well-known from the Traveling Salesman Problem: Miller-Tucker-Zemlin formulation. $$ t_j \ge t_i + 1 + (n-1)(x_{i,j}-1) \ \forall i,j| i\ne \text{source}, j\ne \text{sink}\\ t_i \ge 0\\ $$

Integrity constraint: $$ x_{i,j} \in {0,1}\\ $$

As input parameter we specify start and end node of our path: $$ b_{i} = \begin{cases} 1, \ \text{if i is start/source node}\\ -1, \ \text{if i is end/sink node}\\ 0, \ \text{ else }\\ \end{cases} $$

Tooling

• Pyomo as LP modelling language
• Optimizer: CBC
• NetworkX
• Python

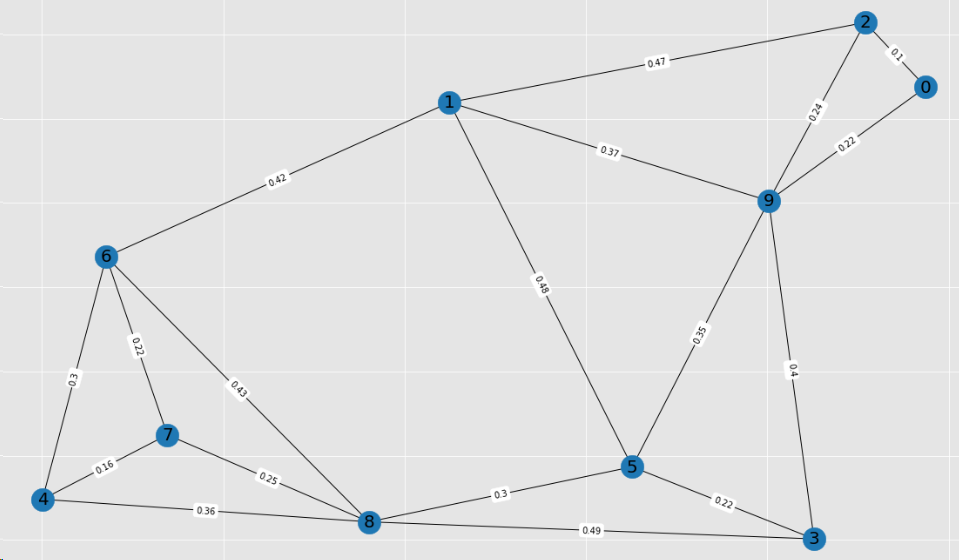
Result

The sum of all edges in our network is 5.7660.

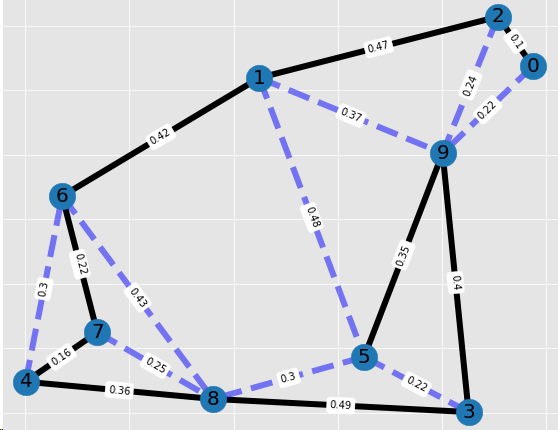
Walking from node 5 to node 0 will give us a workout of distance 2.97652.

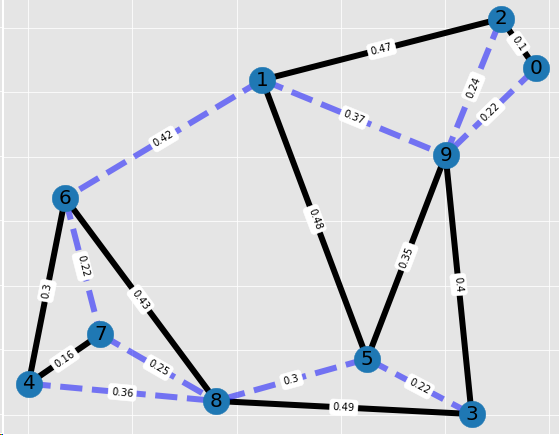
Starting at 7 we can even cover a bigger distance: 3.17453.

For a network this size the optimizer has no difficulty to find the solution in a split-second. However, this is not true for larger real world problems.

Summary

Understanding how to extend a well known TSP Mixed Integer problem formulation to the Longest Path problem provides insights into Linear Programming. Applying NetworkX to handle network topology and visualization added another joyful aspect to this endeavor. Graphs made easy for everybody.

Special thanks to Yet Another Math Programming Consultant, whose blog is an inspiration for everybody who fancies Mathematical Programming.

If you are interested in the Pyomo model or the Python code contact me via mail.