• Partition an \(n \times n\) square into multiple non-congruent integer-sided rectangles.
• The rectangles must be non-congruent and the side length must be an integer number.
• Find the least possible length difference between the largest and smallest used rectangle, i.e. make the rectangles as similar as possible.
• Every rectangle can only be used once.

There is related work covering multiple aspects of the problem and its solution. Here we focus on a Mixed Integer Programming approach.

Artistic Approach

The visualization of solutions to this puzzle bear some resemblance to artwork of to the famous painter Piet Mondriaan. This is the reason why this class of puzzles is associated with his name:

Challenges

The mileage varies with your experience, of course.

1. Understand the problem (easy)
2. Understand a general way to model tiling problems in MIP (medium)
3. Implement the index sets (challenging)
4. Translate the model into Pyomo (medium)
5. Visualize the result (easy)

Tooling

• Pyomo as LP modelling language
• Optimizer: CBC
• matplotlib for visualization
• Python

Model

The following indices characterize the model objects: $$ k = (1,..,K): \ \text{ set of rectangles }\\ r = (0,1): \ \text{ rectangle is rotated (1) or not (0) }\\ i, j = (1,..,N): \ \text{ N is the dimension of the enclosing square } $$

A rectangle is fully characterized by the tuple \((k, r)\). Not all rectangles can be rotated (it does not make sense to rotate a square, or there may not be space left to rotate for a given position).

How to model tiling problems

The partitioning of an area into rectangles requires to answer two questions. To encode this information we deploy two Boolean datastructures ¹.

1. Where can a rectangle be position without violating the bounding square: $$ \mathit{ok}_{k,r,i,j} = \begin{cases} \mathit{Yes} & \text{if we can place rectangle \(k\) at location \((i,j)\)} \\ \mathit{No} & \text{otherwise} \end{cases} $$

2. Which cells \((i’, j’)\) are covered by placing a rectangle \((k, r)\) at \((i, j)\): $$ \mathit{cover}_{k,r,i,j,i’,j’} = \begin{cases} \mathit{Yes} & \text{if cell \((i’,j’)\) is covered by placing rectangle \(k\) at location \((i,j)\)} \\ \mathit{No} & \text{otherwise} \end{cases} $$

The central idea is to construct a parameter set which encodes the information which rectangles cover a particular cell \((i’,j’)\). In our model a rectangle is charcterized by the tuple (k, r, i, j). The following scetch outlines the basic principle with three rectangles, overlapping at cell \((4,3)\).

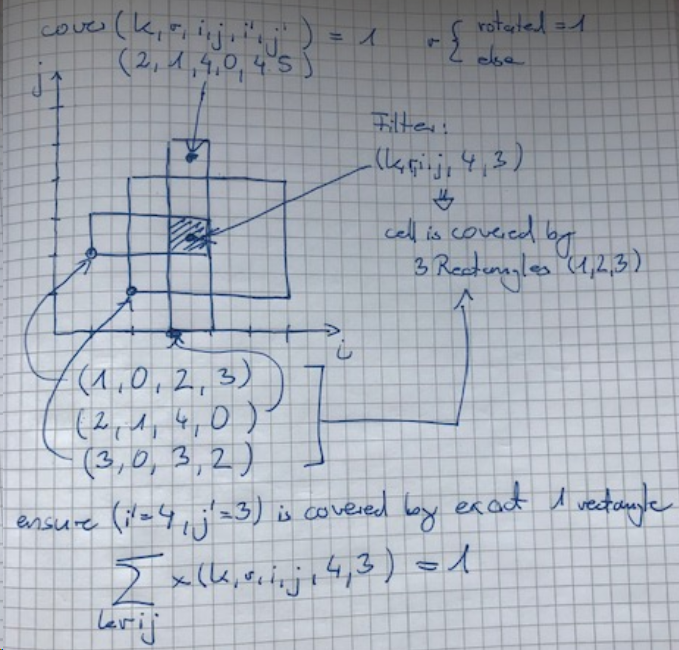
The datastructure \(cover\) allows to filter all rectangles which cover a particular cell \((i’,j’)\) and so provides a means to formulate an overlap constraint elegantly: The sum off over all potential rectangles must be one.

Variables

The decision variables for this partition problem are: $$ x_{k,r,i,j} = \begin{cases} 1 & \text{if rectangle \(k\) (rotated if \(r=\mathrm{y}\)) is placed at location \((i,j)\)} \\ 0 & \text{otherwise}\end{cases} $$

$$ y_{k} = \begin{cases} 1 & \text{if rectangle \(k\) is used} \\ 0 & \text{otherwise}\end{cases} $$

$$ u: \ \text{ upper length: longest rectangle }\\ l: \ \text{ lower length: longest rectangle }\\ $$

Objective

Minimize the difference in length between the longest and shortest rectangle: $$ \min u-l\\ $$

Constraints

Cover all cells \((i’, j’)\): $$ \sum_{k,r,i,j|cover(k,r,i,j,i’,j’)} x_{k,r,i’, j’} = 1, \ \forall i’,j’ \\ $$

Select max one type of rectangle: $$ y_k = \sum_{r,i,j|ok(k,r,i,j)} x_{k,r,i,j}, \ \forall k\\ $$

Bound smallest area: $$ l \le area_k y_k + M(1-y_k), \ \forall k\\ $$

Bound largest area: $$ u \ge area_k y_k \ \forall k\\ $$

Bound total area: $$ \sum_k area_k y_k = n^2\\ $$

Number domain constraints: $$ x_{k,r,i,j} \in {0,1}\\ y_k \in {0,1}\\ u,l \ge 0\\ M = \max_k area_k\\ $$

Pyomo Implementation

Interpretation of the ‘cover all cells’ constraint:
Pick a cell \((i’, j’)\) and sum over all possible rectangles which theoretically could cover it. The constraint enforces that exactly one rectangle will cover that cell.

In Pyomo this constraint looks like (ii, jj stands for \(i’, j’\)):

    def cover_cell_c(model, ii, jj):
        covers = [key for key, _ in cover.items() if (key[4] == ii and key[5] == jj)]
        return sum(model.x[k, r, i, j] for (k, r, i, j, ii, jj) in covers) == 1
    model.cover_cell_c = Constraint(model.I, model.J, rule=cover_cell_c)

This does look simple enough because the inherent complexity is already encoded in the Boolean datastructure cover[k, r, i, j, ii, jj].

The final Pyomo model was surprisingly compact after the indices have been defined correctly.

Of course some matplotlib programming is required in order to provide adequate visualization.

Result

For a \(17 \times 17\) square I reached to optimal solution after 21min compute time on an I7 with 8 cores. The length difference between the smallest and longest rectangle is 8.

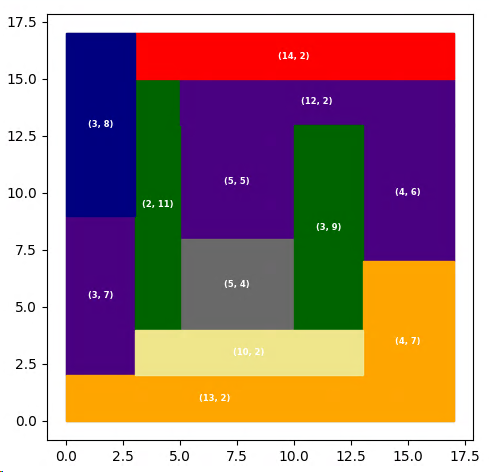
At the time of this writing solutions up until N=57 have been found ².

Summary

The biggest challenge with this puzzle was to understand how to restrict indices in the constraint formulas to viable subsets. The definition and implementation of indices itself is something to get your head around, but then applying these sparse sets in the MIP model is an important skill in solving MIP problems of this type.

Again I have to thank Yet Another Math Programming Consultant for his blog which provides just the right level of detail in order to not provide a full solution, but give enough guidance to find your own way.

Another interesting application of the \(cover\) idea is Another Boring Lockdown Day and Patient Scheduling.

If you are interested in the Pyomo model or the Python code contact me via mail.