Numberlink Puzzle

30 May, 2020

Problem

Connect each two cells with the same numbers by a line.
The sections of a line run horizontally or vertically.
Each cell must be visited exactly once by a line.

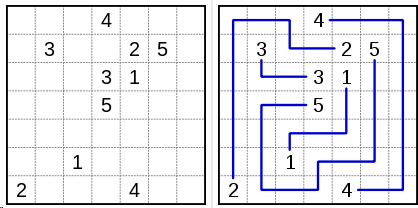
Solution

The trick is to identify endpoints of numberlinks. They do have only one neighbor with the same value. Cells wich are part of a path must have two neighbors with the same value.

The challenge is now to encode this insight into a Mixed Integer Programming model and fire up a solver.

There are different approaches to this problem, not all linear. We are going to implement one from Rob Pratt based on a linearization of a mixed integer quadratically constrained model. If you are interested in the background of the model (and you should!) then please refer to the inspiration for this article: Numberlink Models ¹.

Model

$$ k: \text{number k}\\ p,q: \text{cells}\\ $$

Variables

$$ x_{p,k} = \begin{cases}1 \text{ if cell $p$ has value $k$}\\ 0 \text{ otherwise}\end{cases} $$

Parameters

$$ N_{pq} = \begin{cases} 1, \ \text{ true if p,q are neighbors }\\ 0, \ \text{ else }\\ \end{cases}\\ c_{pk} = \begin{cases} 1, \ \text{ 1 if cell p is an end-point with value k }\\ 0, \ \text{ else }\\ \end{cases} $$

Constraints

$$ \sum_{q|N(p,q)} x_{q,k}=1, \ \text{ if cell $p$ is an end-point with value $k$}\\ $$

$$ 2x_{p,k}\le \sum_{q|N_{p,q}} x_{q,k} \le 2x_{p,k}+M_p(1-x_{p,k}), \ \text{ if cell $p$ is not an end-point} \\ $$

$$ M_p=|N(p,q)|=\sum_{q|N(p,q)} 1, \ \text{ number of neighbors of cell p, at most 4}\\ $$

$$ x_{p,k} = c_{p,k}, \ \text{ if cell p is an end-point}\\ x_{p,k} \in {0,1}\\ $$

Implementation

We need the set of neighbors, which we use as bespoke index $N_{pg}$ in order to formulate the model constraints.

def create_neighbors(self) -> None:
    N = self.dimension
    M = self.dimension
    for i in range(1, N + 1):
        for j in range(1, M + 1):
            if i > 1:
                self.neighbors[i, j, i - 1, j] = 1
            if i < N:
                self.neighbors[i, j, i + 1, j] = 1
            if j > 1:
                self.neighbors[i, j, i, j - 1] = 1
            if j < M:
                self.neighbors[i, j, i, j + 1] = 1

model.N = Set(initialize=[n for n in self.neighbors if self.neighbors[n] == 1])

No we can write the main inequality constraint, i.e. cell $p$ is not an end-point:

def x_lb_c(model, i, j, k):
    if (i, j, k) not in model.L:
        return 2 * model.x[i, j, k] <= sum(
            model.x[iii, jjj, k] for (ii, jj, iii, jjj) in model.N if ii == i and jj == j
        )
    else:
        return Constraint.Skip
model.x_lb_c = Constraint(model.I, model.J, model.K, rule=x_lb_c)

def x_ub_c(model, i, j, k):
    if (i, j, k) not in model.L:
        return sum(model.x[iii, jjj, k] for (ii, jj, iii, jjj) in model.N if ii == i and jj == j) <= \
               2 * model.x[i, j, k] + M * (1 - model.x[i, j, k])
    else:
        return Constraint.Skip
model.x_ub_c = Constraint(model.I, model.J, model.K, rule=x_ub_c)

Additionally, we create a helper index for the given path start- and end-points, which allows us to formulate the corresponding constraint for numberlink edges concise:

model.L = Set(initialize=[(i, j, k) for (i, j), k in self.links.items()])

def x_fixed_c(model, i, j, k):
    if (i, j, k) in model.L:
        return model.x[i, j, k] == 1
    return Constraint.Skip
model.x_fixed_c = Constraint(model.I, model.J, model.K, rule=x_fixed_c)

Result

11 x 11

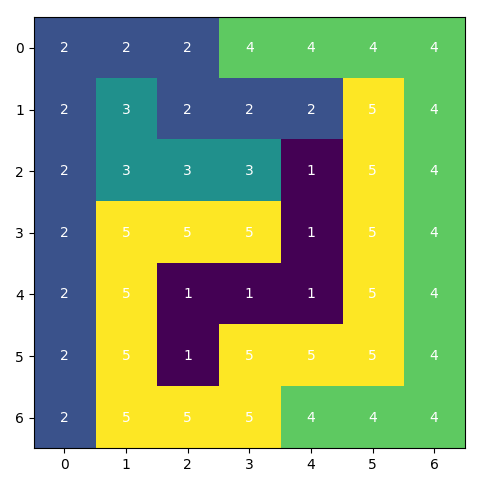
Running the model against this 11x11 puzzle ² was easy for CBC on 6 cores on my virtual machine. The solution took less then 1s.

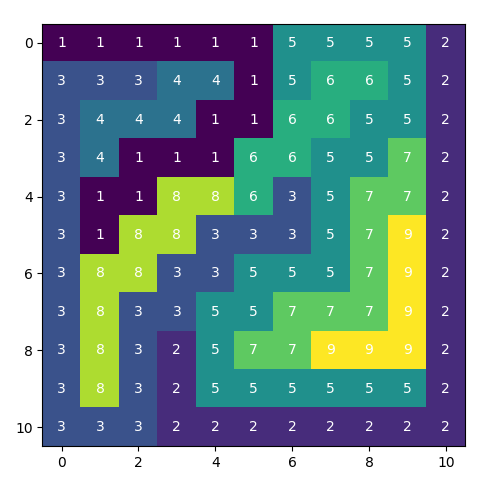
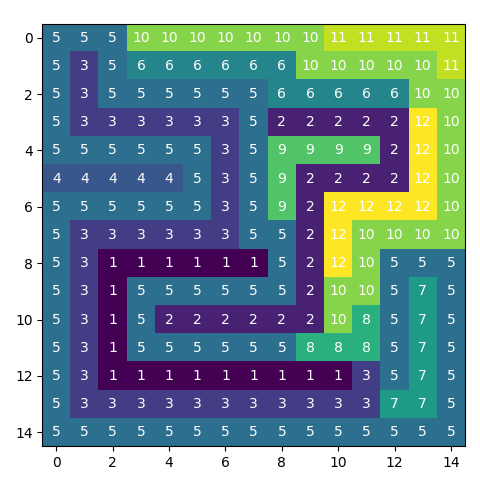
15 x 15

A solution for 15x15 is possible:

Number of constraints : 5625
Number of variables : 2700
Duration: 00:00:40

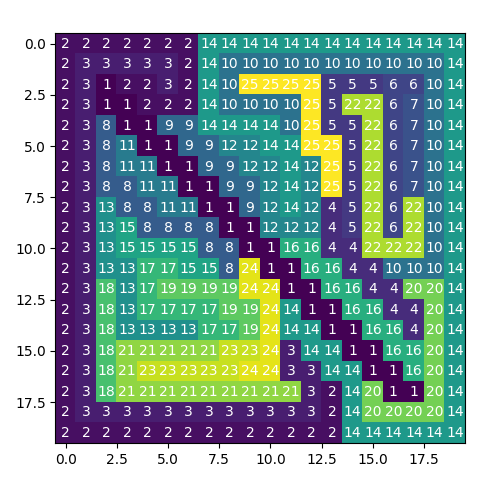
20 x 20

Going for a bigger prize ³ however did not result in a solution with CBC. After 12h I stopped the calculation.

Here the difference between Open Source and commercial solver becomes obvious. With a commercial solver (e.g. CPLEX, Gurobi) the problem can be solved within 43min:

Number of constraints : 20400
Number of variables : 10000
Duration: 00:42:47

Summary

For larger problems CBC MIP solver is not the best tool. For this kind of puzzle SAT solvers might be a better choice ¹.

#python #optimization #pyomo