Select Points

Given multiple sets of data points. Select one point per set so that the distances between the points is minimal.¹

Model

Non-convex MIQP Model

$$ \min \sum_{i,j| ok_{i,j}} dist_{i,j} \cdot x_i \cdot x_j \\ \sum_{i|group_{i,g}} x_i = 1 \forall g \\ x_i \in {0,1} $$

Linear MIP Model

To linearize the model a standard procedure can be applied:

Let’s introduce a new binary variable, $z_{i,j}$, that represents the product of the binary variables $\color{darkred}x_i$ and $\color{darkred}x_j$. This new variable will replace the nonlinear term in the objective function, making the model linear. We will also add constraints to link the new variable $z_{i,j}$ with the original variables $\color{darkred}x_i$ and $\color{darkred}x_j$.

\begin{align} \min&\sum_{i,j|ok_{i,j}} dist_{i,j}\cdot z_{i,j} \\ & \sum_{i|group_{i,g}} x_i = 1 && \forall g\\ & x_i \in {0,1} \\ & z_{i,j} \leq x_i && \forall i,j|ok_{i,j} \\ & z_{i,j} \leq x_j && \forall i,j|ok_{i,j} \\ & z_{i,j} \geq x_i + x_j - 1 && \forall i,j|ok_{i,j} \\ & z_{i,j} \in {0,1} && \forall i,j|ok_{i,j} \end{align}

Implementation

Calculating the sparse $ok_{i,j}$ set is key for a simple Pyomo implementation of the model. With this set and using Pyomo’s decorator syntax the model looks compact:

        m.I = pyo.RangeSet(config['N'])
        m.G = pyo.RangeSet(config['G'])
        m.Ok = pyo.Set(initialize=Ok(config).ok)

        @m.Param(m.Ok)
        def distance(model, i, j):
            p = Point(*self.points[i])
            q = Point(*self.points[j])
            return sqrt((p.x - q.x) ** 2 + (p.y - q.y) ** 2)

        m.groups = pyo.Param(m.G, initialize=group(config))

        m.x = pyo.Var(m.I, domain=pyo.Binary, initialize=0)
        m.pair = pyo.Var(m.Ok, domain=pyo.Binary, initialize=0)

        @m.Constraint(m.G)
        def one_point_per_group(m, g):
            return sum(m.x[i] for i in m.groups[g]) == 1

        @m.Constraint(m.Ok)
        def both_selected(m, i, j):
            return m.pair[i, j] >= m.x[i] + m.x[j] - 1

        @m.Objective(sense=pyo.minimize)
        def total_distance(m):
            return sum(
                m.pair[i, j] * m.distance[i, j] for (i, j) in m.Ok)

Result

The CBC solver has no problems with this model:

• feasible and optimal solution found
• Solution 794.15391509
• Number of constraints : 4476
• Number of variables : 4566
• Duration: 00:00:22

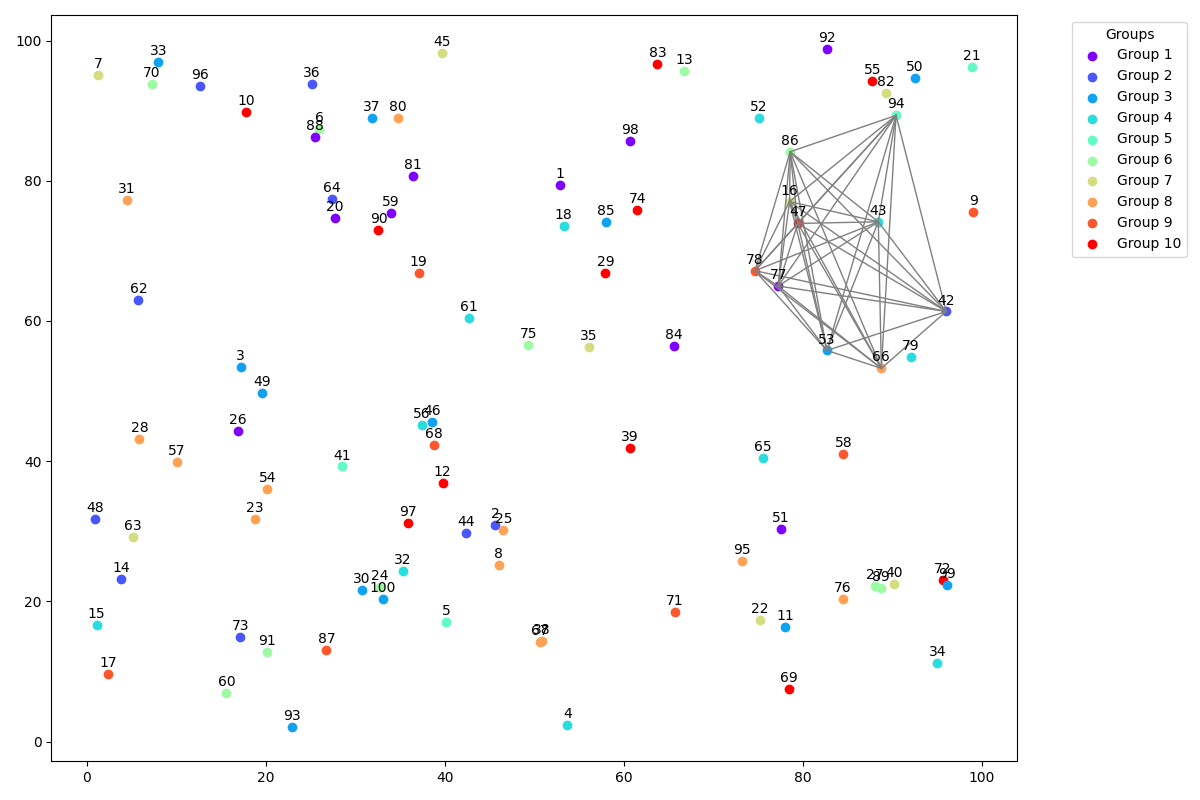
The edges of the 10 solution points are visualized in the graph. The complete code can be found here.

Interesting to see is the solution time between CPLEX ¹ 0.672s and CBC 22s. There is a huge gap between commercial solvers and OSS solvers.

Maximize

Maximizing the same model seems to be much harder for the solver. The same model size as above did not solve within 6000s.

Halve the size solved:

• feasible and optimal solution found
• Solution 777.58370723
• Number of constraints : 2933
• Number of variables : 1026
• Duration: 00:00:33